The beginning of 2021 could make you nostalgic for 2020. First an insurrection at the US Capitol. Then millions of Americans lost power as arctic temperatures blanketed the country. All the while, Covid-19 smoldered in the background. Happy New Year.
Everything is Normal
Charles Perrow, Yale sociologist and expert on complex organizations, wouldn’t be surprised. He knew that in complex systems, accidents are a feature, not a bug.
Inspired by the 1979 near-miss at Three Mile Island, Perrow began studying high-risk systems. His 1984 book Normal Accidents: Living with High-Risk Technologies influenced future thinking on risk and safety. While no Harry Potter, it provides a framework for characterizing risks in complex systems like nuclear power plants or spaceships. In an increasingly interconnected world, his conclusion that catastrophes are a natural by-product of highly complex systems is sobering.
Ominously, Perrow believed that:
We have not had more serious accidents of the scope of Three Mile Island simply because we have not given them enough time to appear. But the ingredients for such accidents are there.
It’s a Relationships Business
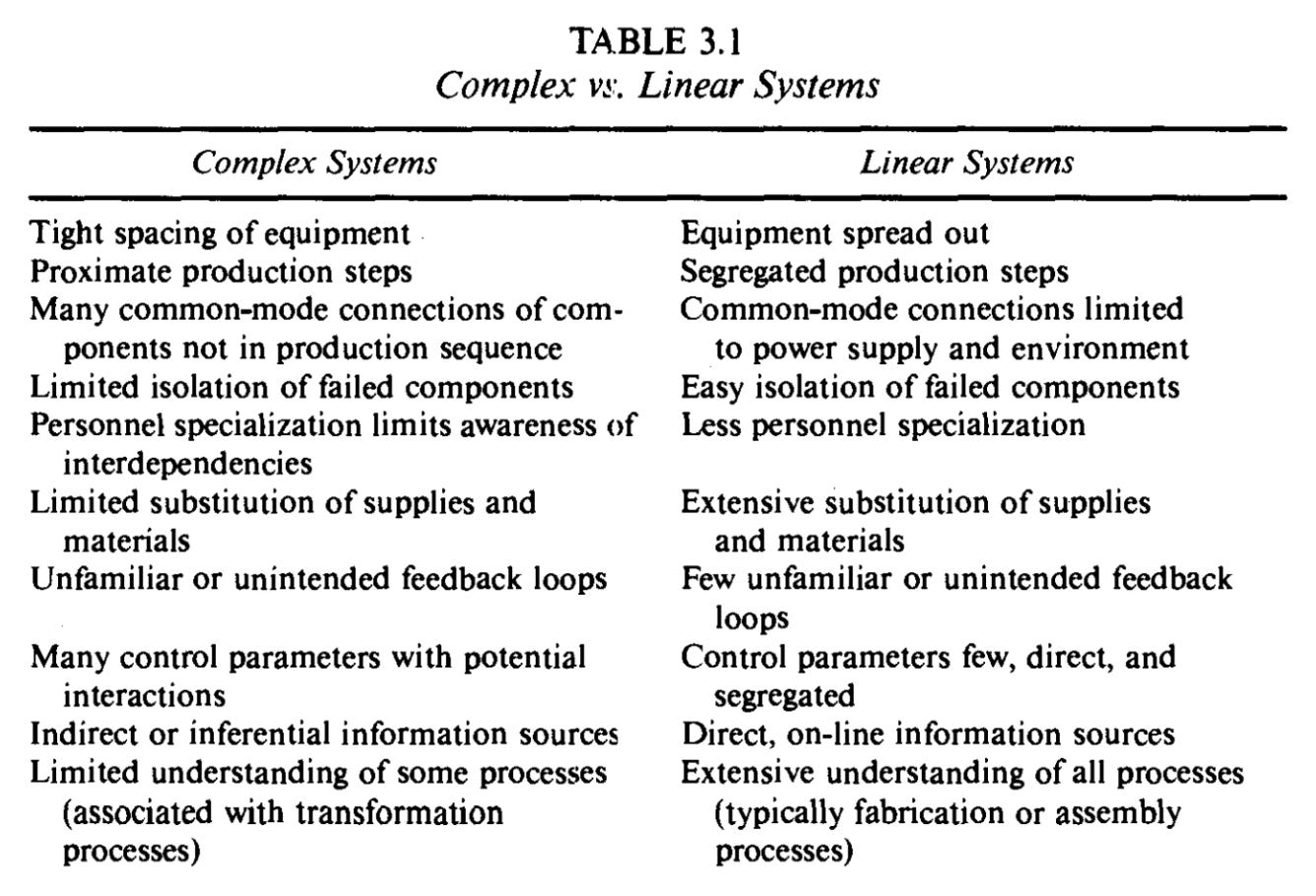
Perrow’s risk assessment framework is a quadrant divided by interactions: linear versus complex; and coupling: loose versus tight. Assembly lines are linear systems. The production sequence is expected and familiar: A then B then C. Components only interact with the things immediately before or after them. Links are few and sequential. Feedback loops are minimal. Parts not in a direct production sequence are spread out. Errors are easy to spot because upstream units pile up or defects appear downstream. Lastly, interdependencies are visible and well understood.
Complex systems are, well, more complex. A nuclear power plant for example. Like linear systems, complex systems can progress from A to B to C. But they can also hop around in unexpected ways: A to orange to zebra. Branching paths, feedback loops, and jumps from one line sequence to another because of proximity mean that connections aren’t alway adjacent or serial. There are multiple paths between parts and the number of paths grows exponentially as the number of parts increases. Information about the state of components or processes is more indirect and inferential. For example, at Three Mile Island, there was no direct measure of coolant levels in the main reactor. Additionally, components often serve multiple functions. Here, a single fault can produce failures in multiple parts of a system, known as a common-mode or common-cause failure. The could come from a broken machine, or the environment, or electricity, as Bloomberg recently reported about the Texas blackouts:
But leaving shale fields like the Permian Basin dark had an unintended consequence. Producers who depend on electricity to power their operations were left with no way to pump natural gas. And that gas was needed more than ever to generate electricity. As one executive described: It was like a death spiral...It’s a phenomenon that highlights just how interconnected - and interdependent - Texas’s energy network is.

No system type is better or worse; they’re just different. Often, necessity drives complexity — it’s the only way to make something. Complex systems are not necessarily high risk. A university is a complex system for example. However, complex systems are riskier than linear systems:
As systems grow in size and in the number of diverse functions they serve, and are built to function in ever more hostile environments, increasing their ties to other systems, they experience more and more incomprehensible or unexpected interactions. They become more vulnerable to unavoidable system accidents.
Crawfish Boils
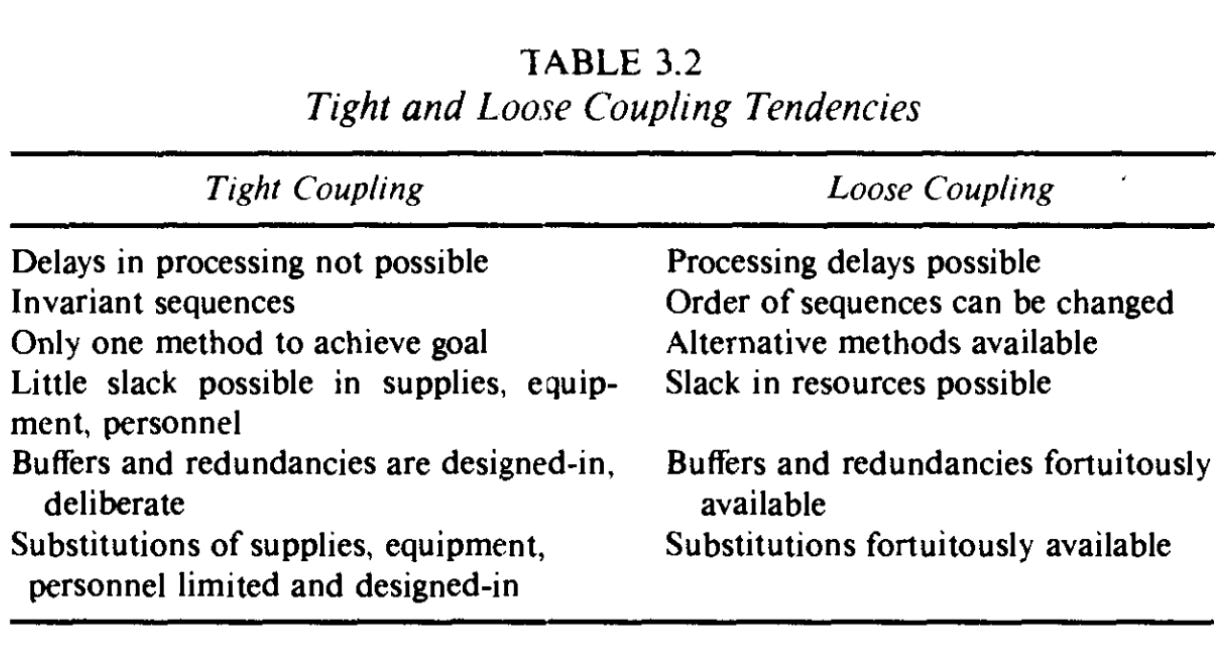
I used to live above a restaurant in the East Village. They had great fried chicken and occasionally threw crawfish boils. It was the sort of place where neighborhood waiters and bartenders hung out after hours. They enjoyed listening to music. Occasionally, loudly. Auditory, my bedroom was tightly coupled with the restaurant below (pro tip: sleep with earplugs). My upstairs neighbors weren’t. With tight coupling there’s no slack or buffer between two items. What happens to one affects the other.
Coupling sounds like something you could talk to your therapist about. In Perrow’s parlance, it’s a measure of slack or flexibility. Tightly coupled systems have little of either. Precision is required. Resources and equipment are specialized and usually can’t be substituted. They have more invariant sequences, meaning that order matters. They’re also more time dependent. A bastardized way to thinking about them is an impatient and stubborn savant.
Loosely coupled systems are more forgiving. Delays won’t alter the outcome. There are more buffers and redundancies. They’re less specialized, so substitutes are available for equipment, inputs, and labor. Lastly, there are multiple paths to a finished product. If you’re building a plane, you can start with the nose, the tail, or the body.
Lollapalooza Effects
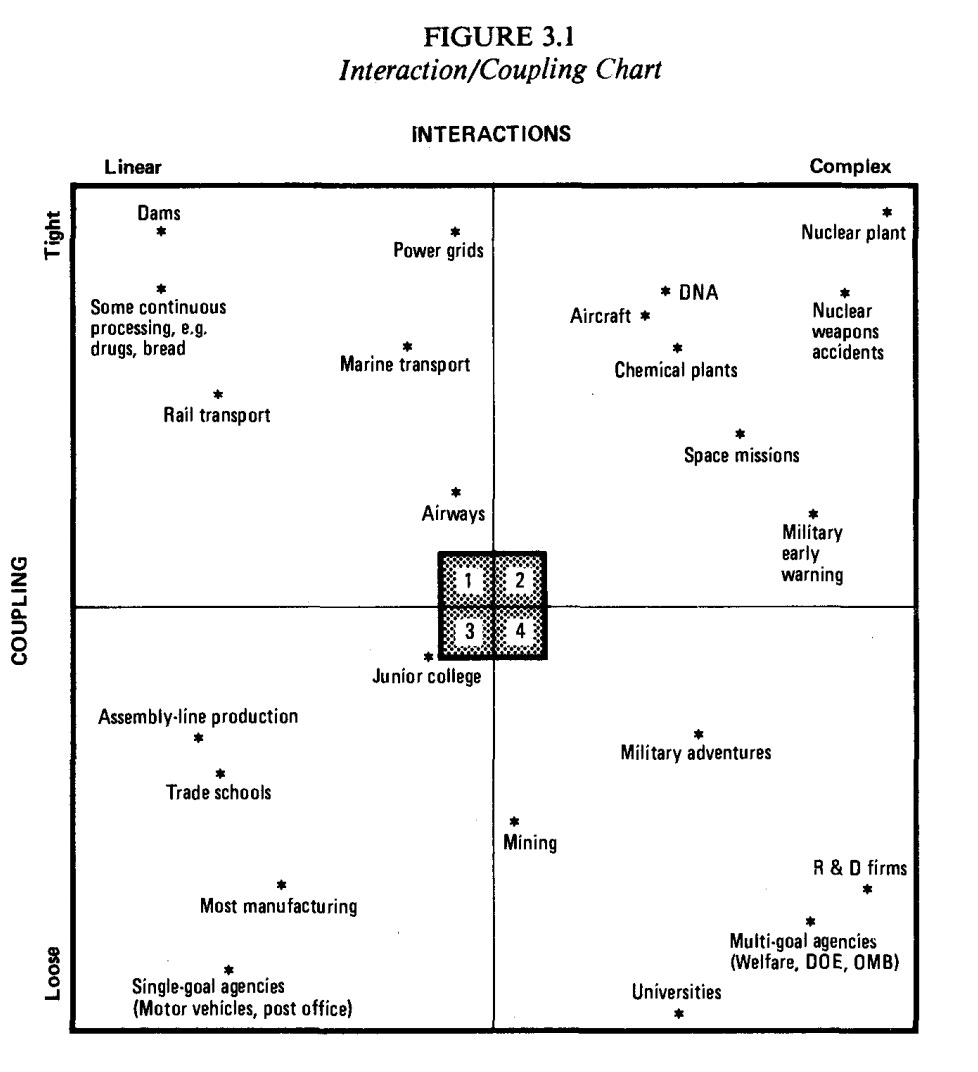
Perrow’s framework is shown below. Danger lies in the top right quadrant. Complex interactions and tight coupling create the conditions for catastrophes, which he called normal accidents.
In part, this is because loosely and tightly coupled systems react differently to stress:
Loosely coupled systems whether for good or ill, can incorporate shocks and failures and pressures for change without destabilization. Tightly coupled systems will respond more quickly to these perturbations, but the response may be disastrous. Both types of systems have their virtues and vices.
Accordingly, engineers and designers devote considerable time to thinking about what could go wrong in tightly coupled systems. This is because safety features need to be deliberately added:
In tightly coupled systems the buffers and redundancies and substitutions must be designed in; they must be thought of in advance. In loosely coupled systems there is a better chance that expedient, spur-of-the-moment buffers and redundancies and substitutions can be found, even though they were not planned ahead of time.
Risk creeps in here. If predicting the future was possible, there would be no problem. But humankind's track record of predicting the future is not great. Because unanticipated interactions are a characteristic of complex systems, it’s impossible for engineers to account for all possible contingencies.
Systems that are most prone to normal accidents have interactiveness, which confuses operators, and tight coupling, which prevents a quick recovery from an accident. Normal accidents involve the unanticipated interaction of numerous failures which creates incomprehensibility. A then orange then zebra instead of A then B then C. If you’ve seen HBO’s excellent/terrifying miniseries Chernobyl, incomprehensibility describes the scenes in the plant's control room.
All normal accidents begin with a single component failure. Most aren’t catastrophic, but sometimes things spiral. To complicate matters, minor issues and catastrophes begin the same way, like how a pitcher uses the same windup whether he’s throwing a fastball or a curveball. Complex interactions and tight coupling increase the odds that a small failure cascades.
Normal accidents are akin to what investor Charlie Munger calls lollapalooza effects. Issues inconsequential in isolation can become explosive in combination:
You get lollapalooza effects when two, three or four forces are all operating in the same direction. And, frequently, you don’t get simple addition. It’s often like a critical mass in physics where you get a nuclear explosion if you get to a certain point of mass — and you don’t get anything much worth seeing if you don’t reach the mass. Sometimes the forces just add like ordinary quantities and sometimes they combine on a break-point or critical-mass basis.
Munger’s message to investors is that they need to understand how things combine and interact. Perrow’s argument is that fully understanding a highly complex system is impossible. Because not all scenarios can be envisioned — arctic temperatures in Texas and many, many others — not all risks can be engineered out. 2022 is a new year, but normal accidents aren’t going anywhere.
Not subscribing would be catastrophic 🤯 🤯 🤯
👉 If you enjoyed reading this post, please share it with friends!





I must become a single goal agency