#70 - Beers with Bezos
Power Laws, Superspreaders and the 80/20 Rule
When Jeff Bezos walks into a bar, the average customer becomes a billionaire. Unfortunately, that fact won’t pay for their next round. Extreme outcomes like Bezos’ net worth are a common characteristic of power law distributions. In a fat-tailed world, averages can mislead.
Watch Your Head, Part 1
Many things in the natural world follow a normal distribution: heights, weights and blood pressure. In a normal distribution, or bell curve, most measures fall around the mean. Move further away from the average in either direction, and occurrences become less likely. For example, the average height of an adult male in the United States is 5 feet, 7 inches1. Most guys you know probably fall within six inches average, a relatively tight range. A man one foot above average is tall enough to play in the NBA, where the average height of a player is 6 feet, 7 inches (in shoes)2.
Even in the most extreme cases, a normal distribution’s range isn’t that wide. Chandra Bahadur Dangi, the shortest adult on record, was 22 inches tall. Robert Wadlow, the world’s tallest man, was 8 feet, 11 inches tall3. The height of the world’s shortest and tallest person are within an order of magnitude of each other. In normal distribution, extreme events are rare. There will occasionally be an eight foot tall person, but never someone who’s eight centimeters or eight miles tall.

Watch Your Head, Part 2
While normal distributions are easy to think about, power laws are flabbergasting. Jeff Bezos’ wealth is equivalent to a man eight miles tall. In a power law, a relative change in one quantity results in a proportional relative change in another. For example, doubling the length of a square from three inches to six inches quadruples its area from nine inches squared (3^2) to thirty-six inches squared (6^2)4.
Power laws crop up in biology, economics, finance, physics, social sciences and other fields. An incomplete list of things that exhibit power laws includes: income distribution, city sizes, earthquake magnitudes, word usage, the distribution of artists by the average price of their works, price fluctuations in stocks, book sales and the intensity of forest fires (measured by acres burned) and wars (measured by casualties).
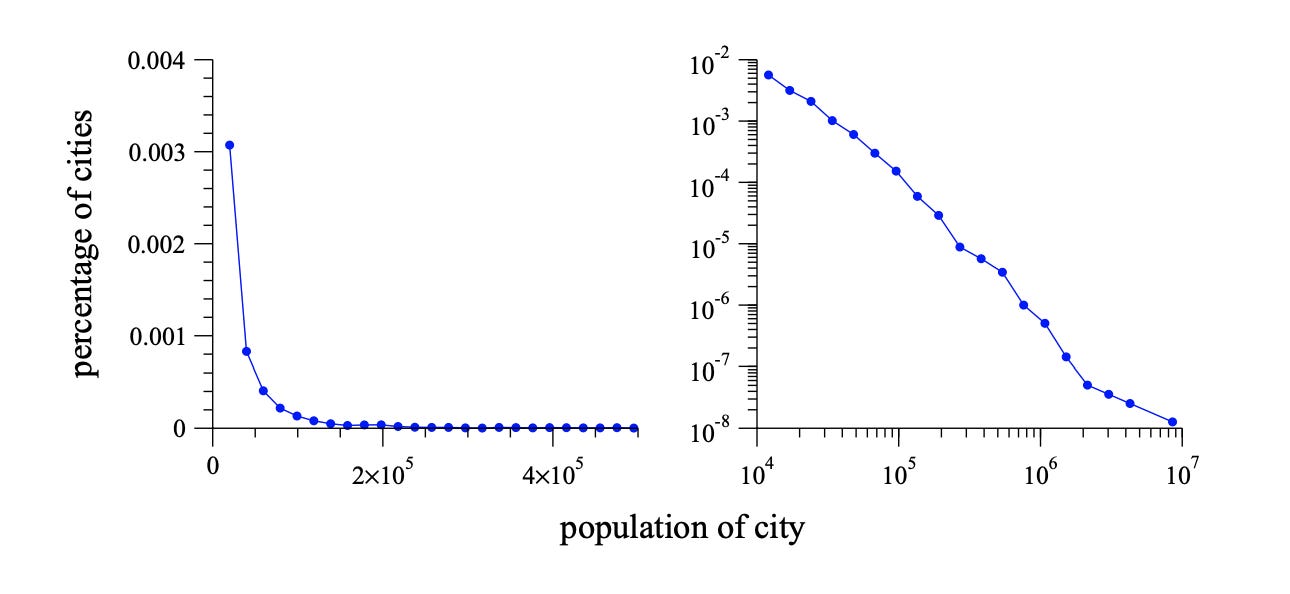
Power laws can lead to non-linear relationships: a small change in one variable can cause a large change in another. Let’s say you’re baking a cake. To double a recipe, you need to double the amount of butter and sugar. That’s a linear relationship: inputs and outputs are proportional. In a kitchen governed by power laws, doubling the amount of butter and sugar could quadruple or sextuple the amount of cake.
Long tails are another characteristic of power laws, meaning extreme outcomes, like Jeff Bezos’ wealth or Tokyo’s population, are expected. In contrast, narrow tails are a characteristic of normal distributions where extreme events are rare. Another way to think about this is the ratio between the minimum and maximum measures. The world’s tallest man was about five times taller than the world’s shortest man. In contrast, New York, the largest city in the US, is eight million times larger than the smallest town (Buford, Wyoming; population: 1). In distributions defined by a power law, the ratio between the average and the maximum can differ by orders of magnitude (see: my bank account versus Jeff Bezos’ bank account). When distributions follow a power law, concepts like average or typical are less helpful to understanding reality compared to a normal distribution.

The 80/20 Rule
One of the best known power laws is the 80/20 rule. In the late nineteenth century, Italian economist Vilfredo Pareto discovered that roughly 80% of Italy’s land was owned by 20% of its population. Pareto found a similar relationship in other countries and even in his vegetable garden where 20% of the pea pods produced 80% of the peas. Pareto’s finding that a majority of consequences comes from a minority of causes was the basis of the 80/20 rule, also known as the Pareto principle.
This dynamic is seen across disciplines. In software development, 20% of modules contain 80% of the bugs. In occupational safety, 20% of the accidents account for 80% of the injuries. In Major League Baseball, the top 15% of players produce 85% of wins above replacement (WAR), a meta statistic that attributes how many wins a player provides relative to an average player over the course of a season5. Lastly, in epidemiology 80/20 logic governs the spread of some diseases, with a few superspreaders accounting for a disproportionate number of transmissions6. An implication of this is that instead of addressing safety concerns, software modules and potentially infectious individuals at random, efforts to identify and target critical nodes have a disproportionate impact.

Another implication of the 80/20 rule is that learning a handful of vital basics can do a lot of heavy lifting. For example, word usage follows a power law. While you won’t win any literary awards, learning the 100 most common words in a foreign language can make you passable. On trips abroad, I’ve gotten a lot of mileage out of the phrases: please, thank you, good morning, two beers please, and where is the bathroom? The flip-side of this is that mastery - the remaining 20% - requires a massive commitment of time and effort. Dos cervezas por favor, señor Bezos.
For more like this once a week, consider subscribing 👇
👉 If you enjoyed reading this post, please share it with friends!

Centers for Disease Control and Prevention. National Health Statistics Reports: Mean Body Weight, Height, Waist Circumference, and Body Mass Index Among Adults: United States, 1999–2000 Through 2015–2016. December 20, 2018.
Wikipedia. Height in Sports. April 3, 2021.
Wikipedia. List of the verified shortest people. Wikipedia. Robert Wadlow, April 3, 2021.
Here’s a more formal mathematical definition from Farnam Street: “A power law is often represented by an equation with an exponent: Y=MX^B. Each letter represents a number. Y is a function (the result); X is the variable (the thing you can change); B is the order of scaling (the exponent), and M is a constant (unchanging). If M is equal to 1, the equation is then Y=X^B. If B=2, the equation becomes Y=X^2 (Y=X squared). If X is 1, Y is also 1. But if X=2, then Y=4; if X=3, then Y=9, and so on. A small change in the value of X leads to a proportionally large change in the value of Y.”
Zimmerman, Jeff (June 4, 2010). Applying the Pareto Principle (80-20 Rule) to Baseball. BeyondTheBoxScore.com.
Superspreader: Galvani, A., May, R. Dimensions of superspreading. Nature 438, 293–295 (2005). https://doi.org/10.1038/438293a

